Modeling Concepts - Degrees of Freedom:
We can describe the position of an atom in space with 3 coordinates: x,y, and z. For a second atom, we need a second set of x,y,z coordinates.
For N atoms, we need 3N coordinates.
This approach gives the absolute positions of atoms in 3D space. However, we typically don't care about the absolute positions of atoms. Instead we usually only care about relative positions of atoms with respect to each other. Because of this, we can ignore those coordinates that correspond to translation and rotation in absolute space and focus only on those coordinates that are internal to the molecule.
In order to understand this, envision one atom, A, at an arbitrary point in space. Now envision a second atom, B. You only need 1 variable (bond length) to describe the position of a 2nd atom relative to the first. Add a 3rd atom, C, and you only need 2 additional variables: a second bond length and an angle. Thus, the relative postions of 3 atoms can be described with 3 variables total. When a 4th atom is added, 3 new variables are required: a bond length, angle and dihedral angle. All additional atoms will require 3 new variables as well.
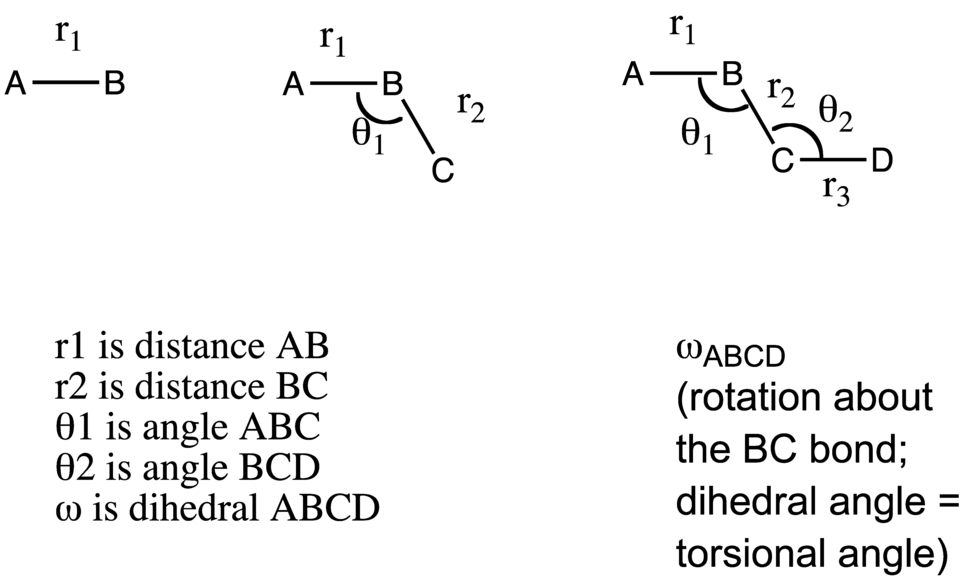
As a general rule, for N bonded atoms, you need 3N-6 terms to describe the internal coordinates for a molecule. This is 3N-5 for a linear molecule.
Summary 1: For a molecule of N atoms, there are 3N-6 internal coordinates. These are N-1 bond lengths, N-2 bond angles, and N-3 dihedral angles (also called torsions). These coordinate variables are called the internal degrees of freedom.
Consider the hypothetical (nonlinear) molecule A-B-C-D. It has (3x4)-6 = 6 degrees of freedom. These are 3 bond lengths, 2 bond angles, and 1 dihedral angle, as depicted in the above figure.
Dihedral Angle: The dihedral angle for ABCD (above) is the angle between the planes ABC and BCD as one looks down the BC axis. In this case, the dihedral angle is 180 degrees. Many people have trouble understanding dihedral angles so this brief section below expands on the topic.
A dihedral angle is an angle between planes. Wikipedia has a pretty good explanation but it is easiest to see in Newman projections for n-butane. If we want to know the CCCC dihedral angle in butane, we must consider the conformations. Here we have the eclipsed and anti forms with the CCCC dihedral angles indicated.
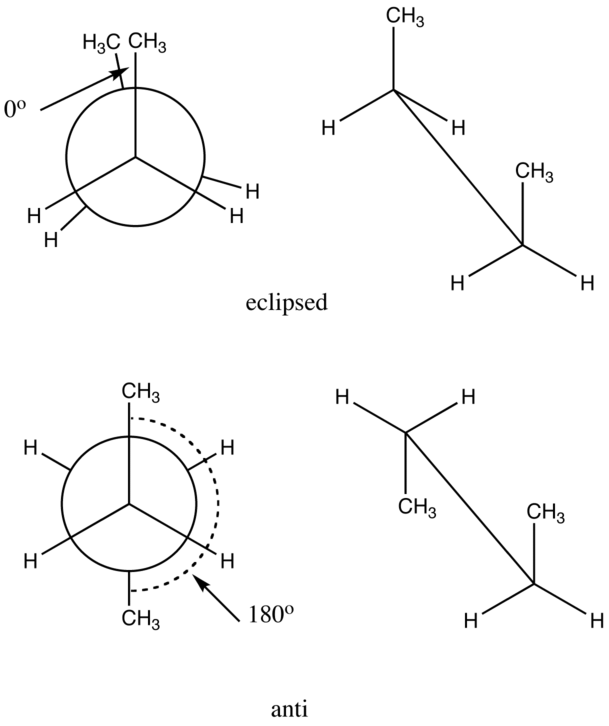
If you rotate around the center C-C bond of butane, and calculate the energy every 10 degrees, you get data that can be plotted as in the graph below. The lowest energy geometry has a dihedral angle of 180 degrees (anti). The highest energy form has a dihedral angle of 0 degrees (eclipsed).
Here are some views made with a molecular modeling program, Maestro.
Butane - eclipsed conformation: dihedral angle = 0 degrees (front view on left, Newman projection like view on right).
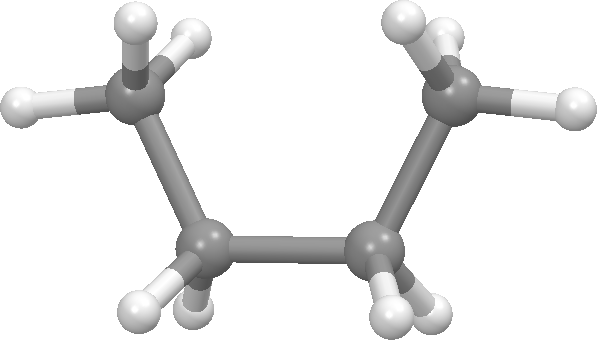
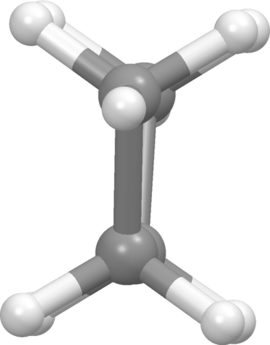
Butane - anti conformation: dihedral angle = 180 degrees (front view on left, Newman projection like view on right).
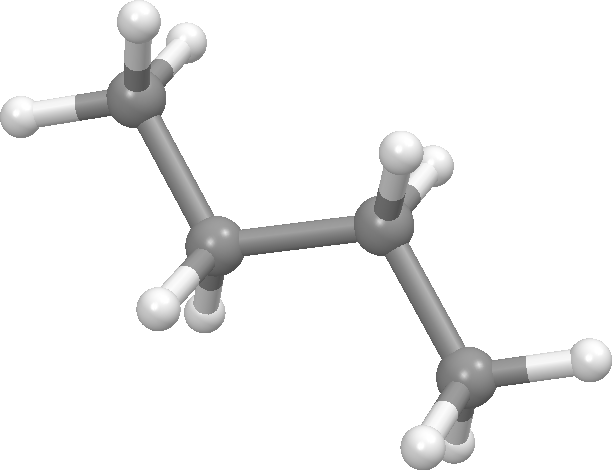
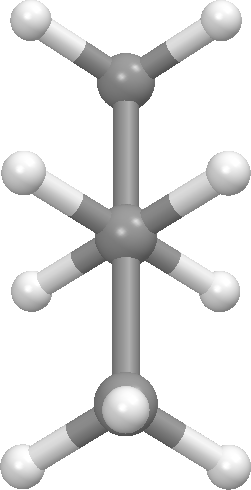
Butane - gauche conformation: dihedral angle = 60 degrees (front view on left, Newman projection like view on right). There is a second gauche conformation at 300 degrees. These are the second lowest energy conformations on the graph.
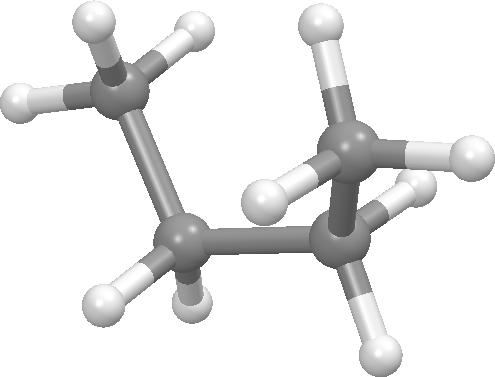
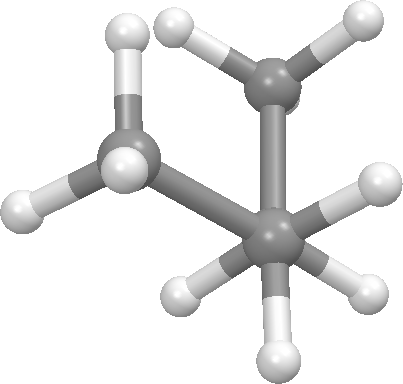
Above we focused on one dihedral angle in n-butane and noted that it has 3 significant conformational states, one anti and 2 gauche. Such states are called conformers, rotamers, or conformational isomers. Bonds that are sp3-sp3 typically have 3 such states. If you are studying a molecule with rotatable bonds, then its conformational flexibility is a key consideration in choosing a molecular modeling method. There is a nice discusion on conformational isomerism at Wikipedia.
Exercise 1: How many internal degrees of freedom are there in n-butane? How many of these are bond lengths, angles and dihedral angles?
Exercise 2: Look at the dipeptide, Anserine. How many rotatable bonds are there? Amide bonds are usually cis or trans (2 conformational states), but sp3-sp3 bonds are usually like butane and have 3 conformational states. Based on that, how many conformational isomers does anserine have overall?
You can go back to the main prelab page or go onto the next concept.