Modeling Concepts - Molecular Miminimization
Thus far we have looked at geometries and energies and how they are related on a potential energy surface. Each of the energy methods we have discussed is capable of finding the energy for a given geometry. Many people are confused by this. By default, when asked to calculate the energy of a molecule, most programs will calculate the energy of whatever geometry is input! This is regardless if it is a great geometry, or some poorly sketched geometry.
In order to get from the input geometry to a geometry of more interest, we have to use an algorithm that will move the geometry. Most people start with a minimization algorithm, also called a geometry optimization algorithm.

Consider a PES for a molecule with 3 low energy conformers like in the above graph. Now look at the graph below where there is a initial geometry indicated at an arbitrary point on the surface.
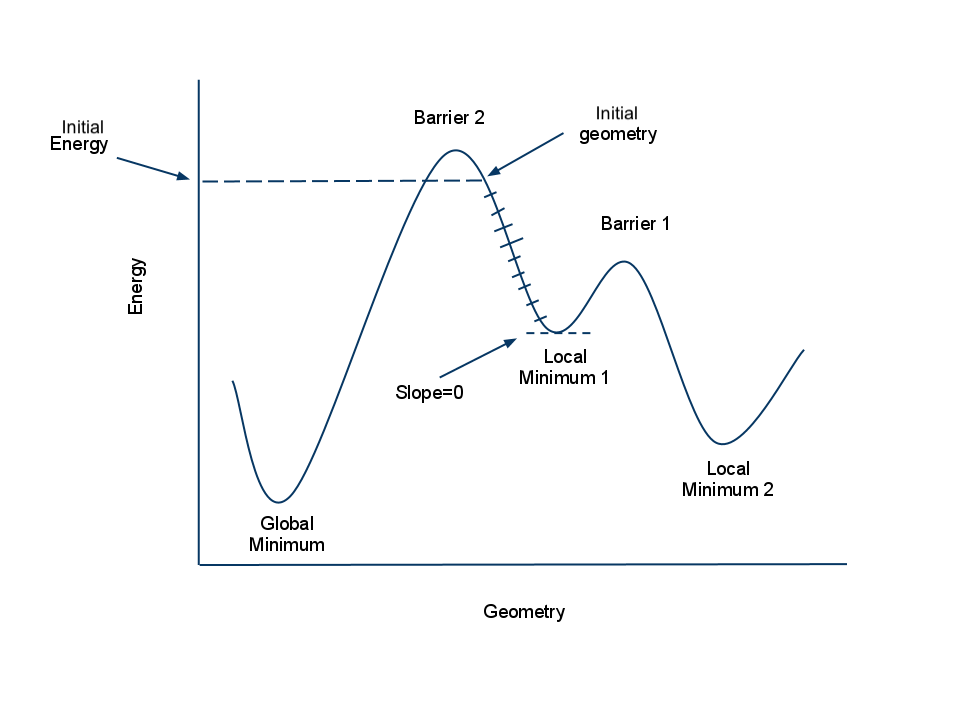
But please realize that we actually have no idea in advance what the PES looks like!
The initial geomtery is
perhaps just something we have sketched so the geometry is not optimized in any way.
And until we calculate the energy, we don't know that either!
If we want to improve the geometry and explore (discover) the PES, we use software to choose both an energy calculation method (quantum mechanics or molecular mechanics) and also choose a minimization algorithm. The energy calculation method calculates the energy for the inital input geometry and for every other geometry the minimization algorithm finds.
Minimizations proceed iteratively. First the initial energy is calculated for the initial geometry. This initial geometry is from your sketch of a molecule or of a file you read in. The minimization algorithm next changes the geometry slightly, trying to reduce the forces acting on the system, and then the energy is recalculated. At each step, the slope of the energy curve (called the gradient) is calculated. The hash marks on the curve indicate intermediate steps (iterations) in the minimization.
The minimization process iterates (calculate energy, change geometry,
calculate energy of new geometry.... repeat) until 1 of 2 criteria are met.
1) The most important criteria is the slope (gradient).
When the slope is
zero (or more commonly, a numerical approximation of zero like 0.005), the algorithm has found a stationary point on the PES.
2) However, in order to prevent calculations from wandering off endlessly in
the event of a flat region of the PES, a maximum number of steps (iterations) is usually also included.
When you set up a minimization, the software usually has default settings to allow enough steps (iterations) for most calculations to get close to a slope (gradient) of zero, while still setting a reasonable upper limit in case of the flat PES problem.
The program output has to be checked at the end of a minimization to see if one has achieved a slope of zero or if one has simply run out of steps. This will make more sense once you start to do calculations.
You should talk to Kathy and Dave about what to do if you run out of steps. Sometimes this is a numerical artefact of a flat PES (common) or a poor input geometry (common), or a maybe it really needs more steps (a little less common but really happens).
As you can see from our example, a minimization algorithm does not necessarily find the global minimum energy structure. It is contingent on the starting geometry. In the next few sections, we'll look at other algorithms that address this issue.
Exercise 6: What happens if you need 347 steps for a minimization to reach a slope of zero, but you only allow it 100 steps? What happens if you need 347 steps for a minimization to reach a slope of zero, but you give it 5000?
You can go back to the main prelab page or go onto the next concept.