Modeling Concepts - Molecular Mechanics:
We looked at the geometry variables on the PES, but what about energy? Molecular mechanics is a way of calculating the relative energies of molecules using classical newtonian mechanics. It works surprisingly well for a wide variety of molecules and here is a nice review article. The potential energy of a molecule can be modeled using 5 simple terms:
E(total) = E(bond stretch) + E(angle bend) + E(torsion) + E(VDW) + E(coulombic)
Most molecular mechanics algorithms have a few more terms, but this is the basic idea. In the sections below, each term is more fully explained.
Bond Stretch
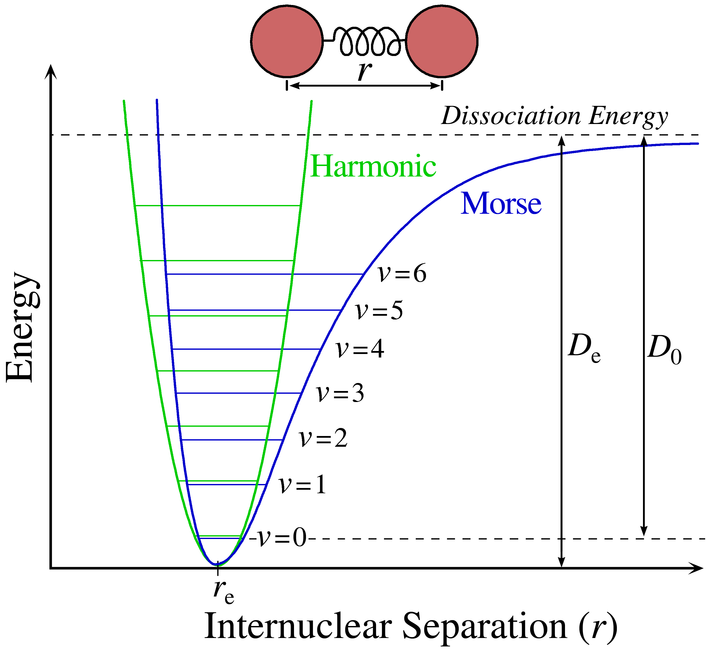
Bond stretch and dissociation can be described using a Morse potential or a Lennard-Jones potential. A Harmonic model overlaps the Morse or Lennard-Jones curves in the low energy states and is essentially a first order term of the Morse potential. The Harmonic model can be expressed using Hooke's Law where the two atoms are treated as balls on an elastic spring.
Ebond stretch = k(r-re)2
In this equation, re is the equilibrium bond length and r is some value away from the equilibrium position. k is the force constant acting to restore the bond. This determines the stiffness of the bond, and the narrowness of the curve. Different types of bonds will have different re and k values. Note also that this equation is per bond. If a molecule has 15 bonds, there will be 15 bond stretch terms total in the overall molecular energy equation.
Angle Bend + Torsion
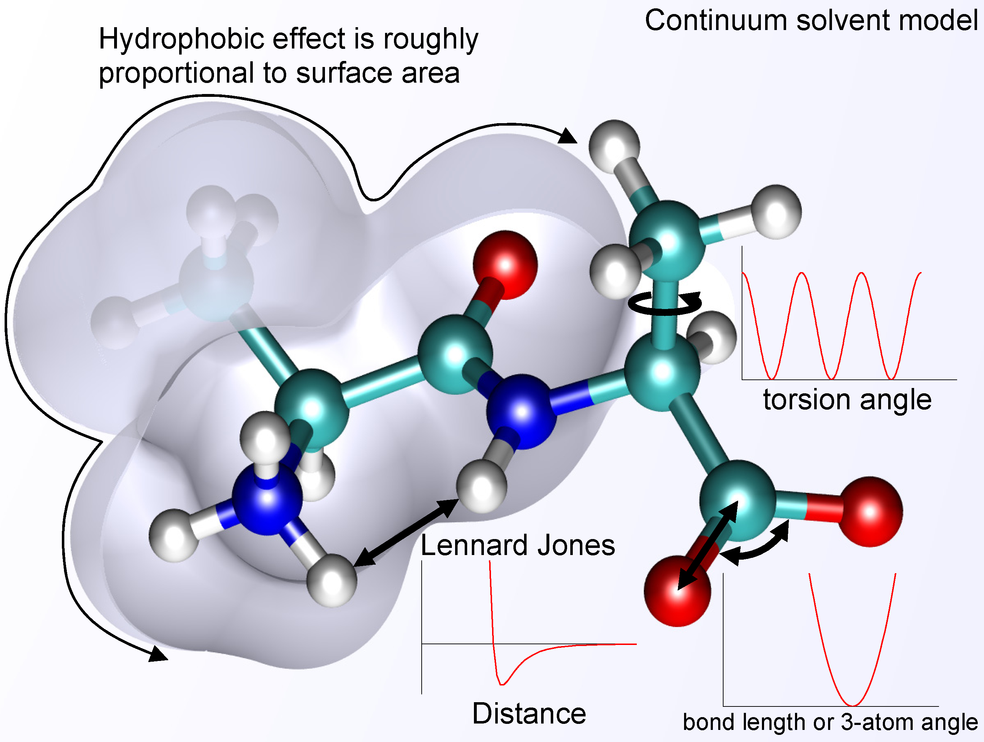
Angle bending is also usually treated as a harmonic potential (lower-right curve in above figure). The k values are usually smaller than in bond stretching since angle bending requires less energy than bond distortion. Torsion is usually treated with a cosine function. Different types of angles and torsions will have different parameters, and again, each angle or torsion will have a term in the overall molecular energy equation.
VDW
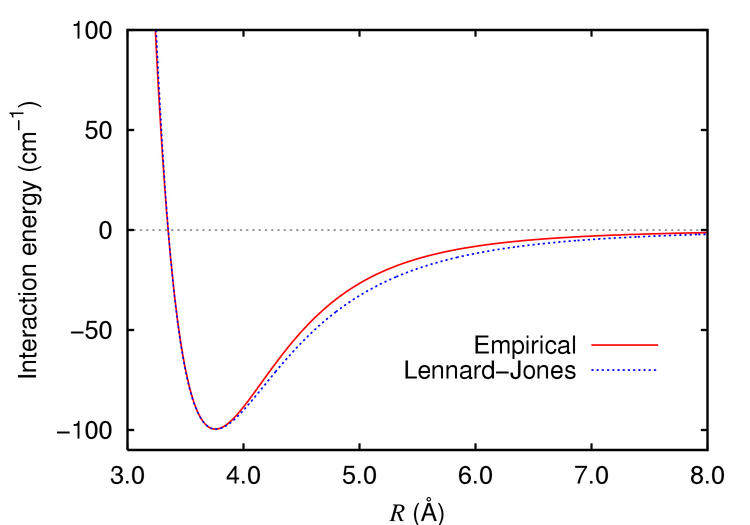
VDW interactions are treated with a simple exponential function (often a Lennard-Jones function) that approximates both attraction and repulsion of neutral atoms. There are parameters for this equation as well, since different atom types will have different VDW radii and electronic structure.
Coulombic
Coulombic (electrostatic) interactions are treated using Coulomb's_law where the atoms are treated as point charges. Sometimes there is continuum solvent model added to mimic water or other solvent.
Summary
Molecular Mechanics treats the potential energy of a molecule using:
E = Ebond stretch + Eangle bend + Etorsion+ EVDW + Ecoulombic
The first 3 terms are atoms that are covalently bonded to each other, whereas the last 2 terms are for "through space" interactions and are usually only applied when atoms are separated by more than 3 bonds.
Consider the above molecule and recall the bond stretch part of the equation:
Ebond stretch = k(r-re)2
This molecule has 22 bonds: (8 x Csp3-H) + (3 x Nsp3-H) + (3 x Csp2-Osp2) + (2 x Csp3-Csp3) + (2 x Csp3-Csp2) + (2 x Csp2-Nsp2) + (1 x Nsp2-H) + (1 x Csp3-Nsp2). Of these bonds, there are 8 unique bond types that require a unique molecular mechanics parameter set, namely a re and k value for each. For example, Csp3-Csp3 re is about 1.54 Angstroms whereas that for a Csp3-Csp2 will be a bit shorter so we need different parameters to model these two different types.
Each bond can move individually though so there are 22 separate bond stretch terms. So for the all the bonds in the molecule:
Ebond stretch (total) = ΣEbond stretch (22 individual bonds)
We could repeat this analysis for the angle bend, torsion, VDW and Coulombic terms and see that a more complete way of writing the Molecular Mechanics Energy equation would be:
Etotal = ΣEbond stretch (total) + ΣEangle bend (total) + ΣEtorsion (total) + ΣEVDW (total) + ΣEcoulombic (total)
***The energy thus calculated is the energy for a particular geometry, a specific arrangement in space of all of the atoms in the molecule, whatever geometry we give as input. The energy is not necessarily an energy of a minimum on the potential energy surface. The molecular mechanics energy equation can be coupled to an algorithm that seeks minima on the potential energy surface but that process is not implicit in the molecular mechanics energy equation itself.***
Exercise 4: How many bonds are there in arginine? How many of those are unique bond types?
You can go back to the main prelab page or go onto the next concept.