Modeling Concepts - Quantum Mechanics
Molecular Mechanics is a simple energy calculation approach, but often we need types of information (HOMO-LUMO energies, reaction energies, etc) that cannot be obtained with MM. So we turn to quantum mechanics. It is impossible to cover quantum mechanics in a single web page so these are just a few key topics.
We use the Schrodinger Equation:
HΨ=EΨ
H = Hamiltonian
E = Energy
Ψ = wavefunction
In order to have any hope of solving this for multiatomic systems, we start with a few approximations. The first is the Born-Oppenheimer approximation. This isolates the electronic portion of the equation from nuclear motion. Nuclei are in a single specified geometry and we calculate the electronic state for that geometry.
The wavefunction is in some ways both an input and an output to this equation. It is built up from molecular orbitals (MOs). MOs can be considered as composed of a linear combination of atomic orbitals (AOs). There are individual AOs for each atom in the molecule. In practice the form of these AOs is expressed as a Basis Set. When you read the literature and you see 6-31+G* for example, this is the basis set, the mathematical functions used to describe the atomic orbitals which form the molecular orbitals. The quality of the output molecular orbitals and energy will be highly dependent on the quality and appropriateness of your basis set.
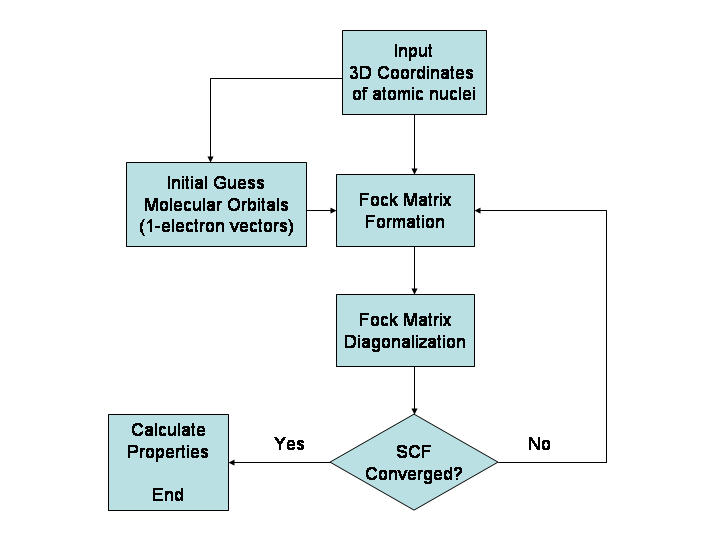
One prevalent way to obtain solutions to the Schrodinger Equation is to use the Variational Method. Given a set of MOs, we can occupy N orbitals at a time, where N is the number of electrons in the molecule. With a reasonable number of MOs, there are many possibilities for the different occupations, which are also called "electron configurations". The variational method begins with a choice for a basic strategy for how the configurations will compose the wavefunction: we can use a general linear combination of them, which involves a great number of coefficients to be determined, or use some scheme to reduce the number of coefficients needed. We thus have various coefficients to be optimized, both for the MOs and the associated configurations. The variational method starts with a guess for these coefficients, then calculates the energy, adjusts the coefficients, and iterates till the lowest-energy set of coefficients is found. Note this wavefunction optimization is just for one geometry. There is no optimization of the geometry implied at this step. One is merely optimizing the wavefunction for a given geometry of interest.
The Hamiltonian includes the description of the physical forces on the system including nuclear-nuclear repulsion, nuclear-electron attraction, and electron-electron repulsion. In computational practice, the form of the Hamiltonian is somewhat bound up with the approaches to solving the Schrodinger Equation, so we'll just move on to that.
A very common approach to solving the Schrodinger Equation is Hartree-Fock (HF). This uses the variational method and uses a single electron configuration. In the Hartree-Fock approach, each electron behaves as though all of the other electrons are a mean field. The electrons are each iteratively optimized with respect to the field of the other electrons. This glosses over many details but a term you will frequently encounter is "SCF", or self-consistent field. When the coefficients of the orbitals are optimized with respect to each other, the system is said to have achieved SCF. Again, there is no geometry optimization implied here, only optimization of a wavefunction for a given geometry.
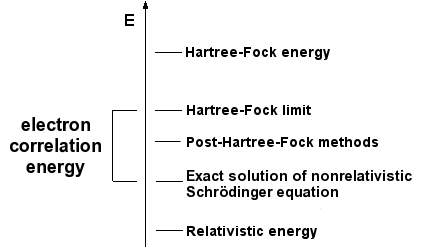
The HF method introduces some errors and this biggest one is electronic correlation. In the HF method, electrons move independently with respect to the field of other electrons, but in fact, electron motions are correlated. This limitation is a consequence of using a single electron configuration; electron correlation enters by including the effects from the other configurations. For example, the LUMO can be occupied instead of the HOMO, and in general, this configuration makes a non-negligible contribution to the wavefunction. There are a wide variety of methods in the literature that correct for electronic correlation and other effects. They are often called post-Hartree-Fock methods. These include MP2, CC, CI, MCSCF, etc. The details are too much for this web page but these methods are computationally challenging. They can be very large and take a very long time.
In the graph below, the top result is an energy from a typical HF calculation. Below that is an energy labeled "HF limit". The HF limit is a HF energy result using the very best basis set to squeeze the absolute most out of the calculation. One could then add in electron correlation and relativistic effects to get closer to the true energy.
Density Functional Theory, DFT, recasts the Schrodinger Equation such that the wavefunction, and thereby the energy, is a "functional" of the Electron Density, ρ.
Ψo = Ψ[ρo]
From this, DFT converts the many-electron Schrodinger Equation into a single-electron Schrodinger Equation. The associated single-electron Hamiltonian is also a functional of electron density and includes separate explicit terms for the so-called exchange and correlation.
Because of this dependence on the density, this reduced Schrodinger Equation must be solved iteratively until SCF is obtained: we guess ρ and then solve for E and the MOs, which define a new ρ, etc. With this, DFT is capable of providing accurate total energies with computational cost roughly similar to that of HF. In practice, we must use some approximate way to the define the exchange and correlation parts of the single-electron Hamiltonian in terms of the density. There are many different examples for this, called "density functionals", and the names for these are often acronyms, e.g. B3LYP. They form a loose hierarchy of approximations. Some of the levels of this hierarchy are shown below with example functionals, in order of increasing complexity from top to bottom:
| Level | Example |
|---|---|
| LDA | SVWN |
| GGA | PBE |
| hybrid | B3LYP |
| meta-GGA | M06-L |
| hybrid meta-GGA | ωB97M-V |
| double hybrid | PBE0-DH |
On average, the higher-level functionals outperform the lower-level ones, but for choosing which functional to use in a given situation, the best practice is to seek literature benchmark data that includes a variety of functionals and is pertinent to the type of chemistry or molecular property, etc., being studied.
Exercise 5: Why use quantum mechanics rather than molecular mechanics?
You can go back to the main page or go onto the next concept.